The Three Body Problem Solved in Unreal Engine 5

The three-body problem is one of those rare physics problems that drastically changed our understanding of the universe as we know it, to the point that is still unsolvable nowadays, and today with the programming skills that I have and Unreal Engine I want to showcase to you how I solved this problem.

Introduction to the problem

Let’s start by stating the problem:

Suppose we have three corpses or “bodies” with mass, all affected by the gravitational pool of the other, and suppose we know their initial positions and momentum, predict the bodies’ future position and momentum at the same time.

Now, if you remember some basic physics principles learned in high school you know Newton’s law of Universal Gravitation:

[math] F = G \frac{m_1 m_2}{r^2}[/math]

But Newton didn’t taught initially to apply his law to three bodies, only after discovering the formula he applied to a more general solution and catatrophy happened.

Lets’ try to do what he did many centuries ago:

Each mass exerts a gravitational force on the others. For three bodies located at positions [math]r1[/math], [math]r2[/math] and [math]r3[/math], the gravitational force on each mass can be expressed as:

[math]\mathbf{F}_1 = G \frac{m_1 m_2}{|\mathbf{r}_2 – \mathbf{r}_1|^3} (\mathbf{r}_2 – \mathbf{r}_1) + G \frac{m_1 m_3}{|\mathbf{r}_3 – \mathbf{r}_1|^3} (\mathbf{r}_3 – \mathbf{r}_1)[/math],

[math]\mathbf{F}_2 = G \frac{m_2 m_1}{|\mathbf{r}_1 – \mathbf{r}_2|^3} (\mathbf{r}_1 – \mathbf{r}_2) + G \frac{m_2 m_3}{|\mathbf{r}_3 – \mathbf{r}_2|^3} (\mathbf{r}_3 – \mathbf{r}_2)[/math],

[math]\mathbf{F}_3 = G \frac{m_3 m_1}{|\mathbf{r}_1 – \mathbf{r}_3|^3} (\mathbf{r}_1 – \mathbf{r}_3) + G \frac{m_3 m_2}{|\mathbf{r}_2 – \mathbf{r}_3|^3} (\mathbf{r}_2 – \mathbf{r}_3)[/math]

From Newton’s second law, the equations of motion for each mass are:

[math]m_1 \frac{d^2 \mathbf{r}_1}{dt^2} = \mathbf{F}_1, \quad m_2 \frac{d^2 \mathbf{r}_2}{dt^2} = \mathbf{F}_2, \quad m_3 \frac{d^2 \mathbf{r}_3}{dt^2} = \mathbf{F}_3[/math]

To solve these equations analytically, we would need to find explicit functions [math]r1(t)[/math], [math]r2(t)[/math], and [math]r3(t)[/math] that describe the positions of the bodies as functions of time. However, we can’t obtain an analytical solution due to the nonlinear and coupled nature of these differential equations.

Ok but what does it mean?

It means that having a system where three or more bodies move them attracted by gravity is unpredictable and chaotic, which tells us that the equation’s solution is impossible!

We can’t describe with absolute precision the motion of more bodies that interact with each other by gravity, and even if we found one the smallest change on the initial conditions of one of the bides can collapse everything we did before.

This means, for example, that the solar system is not as stable and predictable as we think after all.

Bonus: The approach of Henri Poincaré

Poincaré, instead of solving the equation tried to analyze the system’s behavior, introducing the concept of phase space: a geometric representation of the space that allowed him to visualize the possible states (stable or not stable) of a system. Here, each possible configuration of the bodies’ positions and velocities corresponds to a unique point.

Through this approach, he discovered that the three-body problem exhibits sensitivity to initial conditions: small differences in the starting positions or velocities of the bodies grow rapidly over time, leading to vastly different trajectories. With Poincaré Chaos Theory has born, revealing that even simple systems governed by deterministic laws could behave unpredictably.

Moreover, he found that the system’s paths in phase space could form beautiful and intricate patterns, which he called homoclinic tangles. These patterns, where trajectories repeatedly approach and diverge from one another in complex, non-repeating ways, showed that the system could exhibit chaotic, non-periodic motion instead of settling into a predictable cycle.

So if the problem is unpredictable and still unsolvable how do you solve it?

Well, is true that we can’t solve the Three-body problems with a neat mathematical formula that works for every scenario (the general solution we were talking about), but this doesn’t mean that we can predict the motion of the corpses with a very good approximation. And with the technologies and the large amount of computer calculations we can use it for good.

The Special Solution of Three-Body Problem

For Special we mean that we are examining a particular case of the problem.

We can’t calculate the position of three bodies simultaneously, but this is not true for just two of the bodies in consideration.

Using the gravitational laws of Newton we will calculate the position of two of the three bodied and move them by an instant (in Unreal we use Tick) and we do the same for the other combinations of the bodies in the scene. This method is called the Euler’s Method.

Enough math, let’s see some code:

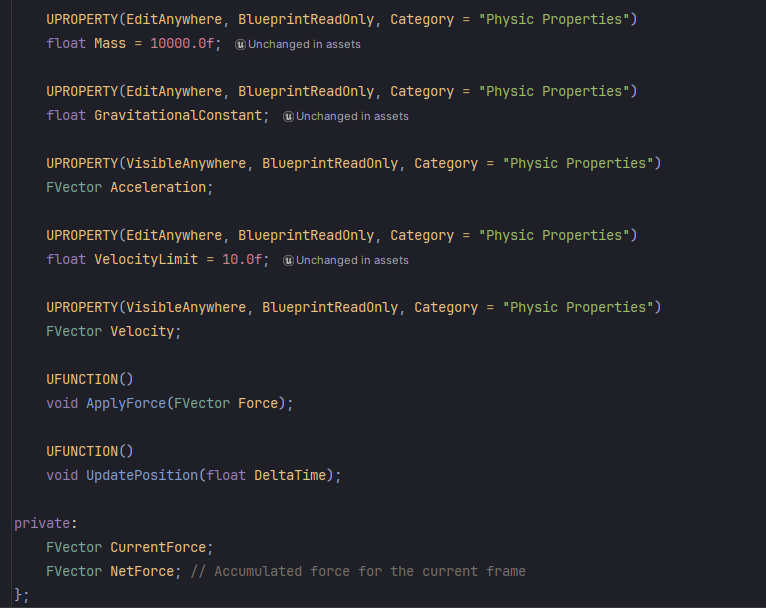
I created the Body class, which contains all the information about the corpse:

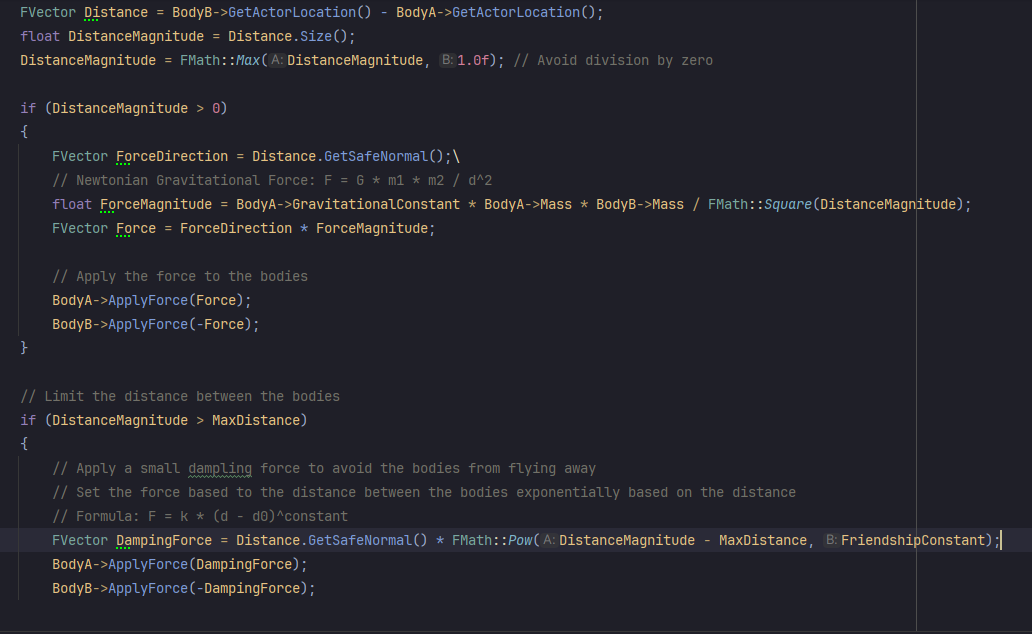
And in the Gamemode I created a special function called CalculateGravitationalForces(), which apply the forces to each pair of body every Tick:

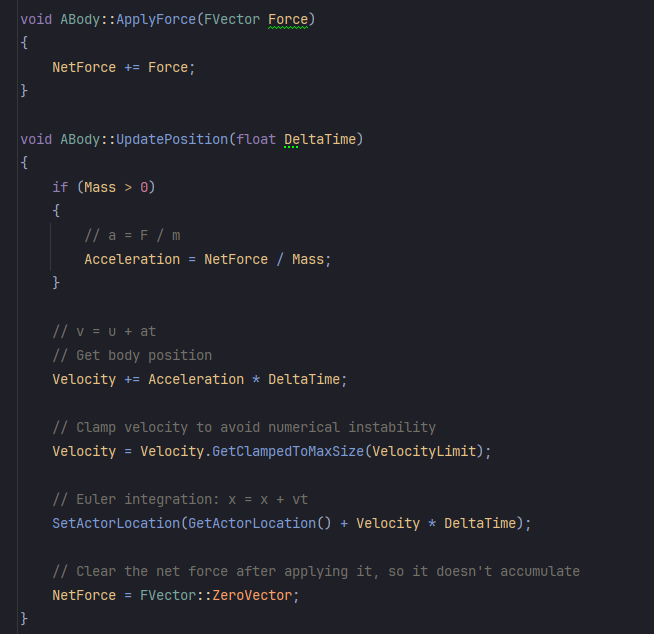
Finally, lets move the pair of bodies:

And put these objects in the game. Here I added to them a glow material to resemble little suns and a Particle Trail to trace their path when they move

And here we go: Three Bodies moving in the environment of Unreal Engine!

Notice how each time at runtime we have different paths

Solving the Three Body Problem in Unreal Engine